Pembahasan Soal Analisis Real Himpunan dan Fungsi: Bagian 1.1

Last Updated on Mei 17, 2025 by prooffic

Postingan kali ini akan menyajikan tentang Pembahasan Soal Analisis Real Himpunan dan Fungsi bagian 1.1. Soal berikut diambil dari buku “Introduction to Real Analysis” oleh Robert G. Bartle dan Donald R. Sherbert.

**Selamat Menikmati**

Berikut ini adalah Pembahasan Soal Analisis Real Himpunan dan Fungsi Bagian 1.1.

Soal 1

Misalkan $A:= \{ k : k\in \mathbb{N}, k \leq 20 \}, B:= \{ 3k – 1 : k \in \mathbb{N} \}$ dan $C := \{2 k + 1 : \mathbb{N}\}$. Tentukan himpunan-himpunan berikut.

1. $A \cap B \cap C,$
2. $(A \cap B) \setminus C,$
3. $(A \cap C) \setminus B$

Jawab. Sebelumnya, semesta pembicaraan pada soal ini adalah himpunan bilangan asli. Untuk memudahkan dalam menjawab soal tersebut, kita terlebih dahulu menuliskan himpunan tersebut dengan cara mendaftar anggota-anggotanya sebagai berikut.

$$\begin{aligned} A & := \{ k \in \mathbb{N}, k \leq 20\} = \{ 1, 2, …, 20 \} \\ B & := \{3k – 1 : k \in \mathbb{N}\} = \{ 2, 5, 8, 11, 14, 17, 20, … \} \\ C & := \{ 2k + 1 : k \in \mathbb{N} \} = \{ 3, 5, 7, 9, 11, 13, 15, 17, 19, …\} \end{aligned}$$

1. Dari definisi himpunan tersebut, dapat dilihat bahwa $$A \cap B = \{ 2, 5, 8, 11, 14, 17, 20 \} $$Kemudian, perhatikan bahwa $C$ adalah himpunan bilangan ganjil yang lebih dari $2.$ Dari sini, untuk menentukan $A \cap B \cap C$ kita cukup mengambil bilangan ganjil yang lebih dari $2$ pada $A \cap B$. Oleh karena itu, $$A \cap B \cap C = \{ 5, 11, 17 \}$$
2. Untuk menjawab soal bagian kedua, terlebih dahulu kita ubah bentuk $(A \cap B) \setminus C$ menjadi $$(A \cap B) \cap C^c = A \cap B \cap C^c. $$Dari sini, untuk menentukan $A \cap B \cap C^c$, cukup mengambil anggota $A \cap B $ yang bukan di $C$ sehingga diperoleh $$(A \cap B) \cap C^c = A \cap B \cap C^c = \{ 2, 8, 14, 20 \}$$
3. Perhatikan bahwa $$A \cap C := \{3, 5, 7 , 9, 11, 13, 15, 17, 19 \}. $$Kemudian, $(A \cap C) \setminus B$ diperoleh dengan menghilangan anggota $B$ di $A \cap C$ sehingga diperoleh $$(A \cap C) \setminus B = \{ 3, 7, 9, 13, 15, 19 \}$$

Baca Juga:
Pembahasan Soal ONMIPA/KNMIPA Analisis Real
Pembahasan Soal ONMIPA/KNMIPA

Soal 2

Gambarkan diagram untuk menyederhanakan dan mengidentifikasi himpunan-himpunan berikut.

1. $A \setminus (B \setminus A),$
2. $A \setminus (A \setminus B),$
3. $A \cap (B \setminus A)$.

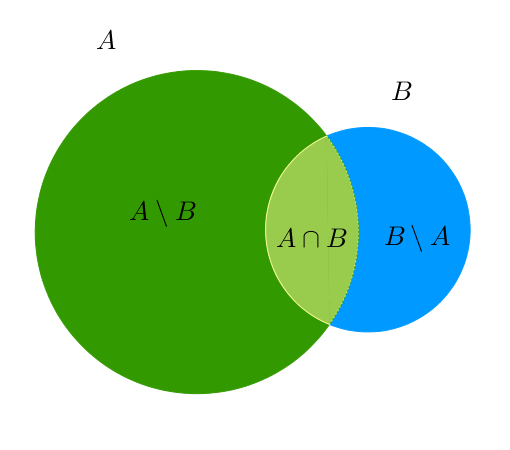
Jawab. Berdasarkan definisi, yaitu $X \setminus Y$ bermakna mengambil anggota $X$ yang bukan merupakan anggota $Y,$ dan diagram tersebut, diperoleh bahwa

1. $A \setminus (B \setminus A) = A,$
2. $A \setminus (A \setminus B) = A \cap B,$
3. $A \cap (B \setminus A) = \emptyset$.

Kita juga akan menunjukkan ketiga identitas di atas dengan menggunakan sifat-sifat himpunan, yaitu sebagai berikut.

1. Perhatikan bahwa dengan sifaft distributif, $$ \begin{aligned} A \setminus ( B \setminus A ) &= A \cap ( B \setminus A )^c \\ & = A \cap ( B \cap A^c )^c \\ & = A \cap ( B^c \cup ( A^c )^c ) \\ & = A \cap ( B^c \cup A ) \\ & = ( A \cap B^c ) \cup ( A \cap A ) \\ & = ( A \cap B^c ) \cup A \\ & = A \end{aligned}$$
2. Perhatikan bahwa dengan sifaft distributif, $$ \begin{aligned} A \setminus (A \setminus B) &= A \cap ( A \setminus B )^c \\ & = A \cap ( A \cap B^c)^c \\ & = A \cap ( A^c \cup ( B^c )^c ) \\ & = A \cap ( A^c \cup B ) \\ & = ( A \cap A^c ) \cup ( A \cap B ) \\ & = ( \emptyset ) \cup ( A \cap B )  \\ & = A \cap B \end{aligned}$$
3. Perhatikan bahwa dengan sifaft distributif, $$ \begin{aligned} A \cap ( B \setminus A ) &= A \cap ( B \cap A^c ) \\ & = A \cap B \cap A^c \\ & = \emptyset \end{aligned}$$

Soal 3

Jika $A$ dan $B$ adalah himpunan, buktikan bahwa $A \subseteq B$ jika dan hanya jika $A \cap B =A.$

Jawab. Terlebih dahulu asumsikan bahwa $A \subseteq B.$ Akan ditunjukkan bahwa $A \cap B =A.$

Jelas bahwa $A \cap B \subseteq A$. Karena $A \subseteq B$ da $A \subseteq A,$ maka $A \subseteq A \cap B.$

Secara keseluruhan, $A \cap B \subseteq A$ dan $A \subseteq A \cap B.$ Berdasarkan definisi kesamaan dua himpunan diperoleh bahwa $$A \cap B = A.$$

Sebaliknya, asumsikan bahwa $A \cap B = A.$ Akan ditunjukkan bahwa $A \subseteq B.$

Diberikan $x \in A.$ Karena $A \cap B = A$ dan $x\in A,$ maka $x \in A \cap B$. Dari sini, $x \in B.$

Secara keseluruhan, jika $x \in A,$ maka $x \in B.$ Oleh karena itu, $A \subseteq B.$

Jadi,  $A \subseteq B$ jika dan hanya jika $A \cap B =A.$

Soal 4

Buktikan hukum De Morgan kedua (Teorema 1.1.4(b)).

Jawab. Hukum De Morgan kedua menyatakan bahwa $$A \setminus ( B \cap C ) = ( A \setminus B ) \cup ( A \setminus C ). $$Untuk menunjukkan kesamaan tersebut, cukup ditunjukkan bahwa $$A \setminus ( B \cap C ) \subseteq ( A \setminus B ) \cup ( A \setminus C ) $$ dan $$( A \setminus B ) \cup ( A \setminus C ) \subseteq A \setminus ( B \cap C ).$$

Terlebih dahulu diberikan $x \in A \setminus ( B \cap C ).$ Maka, $x \in A$ tetapi $x \notin B \cap C$ yang ekuivalen dengan $x \in (B \cap C )^c = B^c \cup C^c.$ Dari sini, $x \in A$, tetapi $x \notin B$ ataupun $x \notin C.$ Oleh karena itu, $x \in A$ dan $x \notin B$, ataupun $x \in A$ dan $x \notin C.$

Akibatnya, $x \in A \setminus B$ ataupun $x \in A \setminus C.$ Dari sini, $x \in (A\setminus B)\cup(A\setminus C).$ Secara keseluruhan, jika $x \in A \setminus ( B \cap C ),$ maka $x \in (A\setminus B)\cup(A\setminus C)$ yang berakibat bahwa $$A \setminus ( B \cap C ) \subseteq ( A \setminus B ) \cup ( A \setminus C ).$$

Sebaliknya, diberikan $x \in ( A \setminus B ) \cup ( A \setminus C )$. Maka, $x \in (A\setminus B)$ ataupun $x\in (A\setminus C).$ Dari sini, $x \in A$ tapi $x \notin B$, atau $x \in A$ tapi $x \notin C.$

Oleh karena itu, $x \in A$, tapi $x \notin B$ atau $x \notin C.$ Dengan kata lain, $x \in A$, tapi $x \in B^c$ atau $x \in C^c$.

Oleh karena itu, $x \in A$ tetapi $x \in B^c \cup C^c = (B\cap C)^c.$ Akibatnya, $x \in A \setminus (B\cap C).$

Secara keseluruhan, jika $x \in ( A \setminus B ) \cup ( A \setminus C )$, maka $x \in A \setminus (B\cap C).$ Dari sini, $$( A \setminus B ) \cup ( A \setminus C ) \subseteq A \setminus ( B \cap C ). $$Berdasarkan definisi kesamaan dua himpunan, diperoleh bahwa $$( A \setminus B ) \cup ( A \setminus C ) = A \setminus ( B \cap C ).$$

Soal 5

Buktikan hukum distributif berikut:

1. $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
2. $A \cup (B \cap C) = (A \cup B) \cap (A \cup C).$

Jawab. Dalam membuktikan kedua kesamaan tersebut, kita akan menggunakan notasi logika matematika.

1. Perhatikan bahwa $$\begin{aligned} x \in A \cap (B \cup C) & \Longleftrightarrow x \in A \land ( x \in B \cup C) \\ & \Longleftrightarrow x \in A \land (x \in B \lor  x\in C) \\ & \Longleftrightarrow (x \in A \land x \in B) \lor (x \in A \land x \in C) \\ & \Longleftrightarrow x \in A \cap B \lor x \in A \cap C \\ & \Longleftrightarrow x \in (A \cap B) \cup (A \cap C)\end{aligned}.$$
   Ini menunjukkan bahwa $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$ ♦
2. Perhatikan juga bahwa $$\begin{aligned} x \in A \cup (B \cap C) & \Longleftrightarrow x \in A \lor ( x \in B \cap C) \\ & \Longleftrightarrow x \in A \lor (x \in B \land  x\in C) \\ & \Longleftrightarrow (x \in A \lor x \in B) \land (x \in A \lor x \in C) \\ & \Longleftrightarrow x \in A \cup B \land x \in A \cup C \\ & \Longleftrightarrow x \in (A \cup B) \cap (A \cup C)\end{aligned}.$$
   Ini menunjukkan bahwa $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$ ♦

Soal 6

Selisis simetri dari dua buah himpunan $A$ dan $B$ adalah himpunan $D$ yang terdiri dari semua elemen baik yang ada di $A$ atau di $B$, tetapi tidak di keduanya. Representasikan $D$ dengan diagram.
1. Tunjukkan bahwa $D = (A \setminus B) \cup (B\setminus A).$
2. Tunjukkan bahwa $D$ juga diberikan oleh $D = (A \cup B) \setminus (A \cap B).$

Jawab. Misalkan $A$ dan $B$ adalah dua buah himpunan. Maka, $D$ dapat direpresentasikan sebagai bagian berwarna hijau pada gambar berikut.

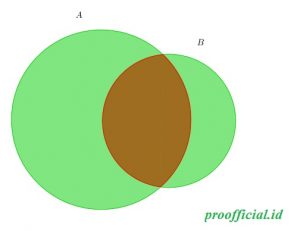
1. Dari definisi, $D$ adalah himpunan yang terdiri dari semua elemen baik yang ada di $A$ atau di $B$, tetapi tidak di keduanya. Dengan kata lain, jika $x \in D$, maka $$(x \in A \lor x \in B) \land (x \notin A \cap B).$$
   Dengan kata lain, $$x \in (A \cup B) \land x \in (A \cap B)^c. $$Oleh karena itu, $$x \in (A \cup B) \cap (A \cap B)^c $$dan berdasarkan hukum distributif, $$\begin{aligned}D &= (A \cup B) \cap (A \cap B)^c \\ & = (A \cup B) \cap (A^c \cup B^c) \\ & = ((A \cup B)\cap A^c) \cup ((A \cup B) \cap B^c) \\ & = (B \cap A^c) \cup (A \cap B^c) \\ & = (B \setminus A) \cup (A \setminus B) \\ & = (A \setminus B) \cup (B\setminus A)\end{aligned}$$
2. Berdasarkan pembahasan sebelumnya, maka $$ D = (A \cup B) \cap (A \cap B)^c. $$Dari sini, $$D = (A \cup B) \setminus (A \cap B).$$

Soal 7

Untuk setiap $n \in \mathbb{N},$ misalkan $A_n = \{(n+1)k : k \in \mathbb{N}\}$.

1. Tentukan $A_1 \cap A_2.$
2. Tentukan himpunan $\cup \{A_n : n\in\mathbb{N}\}$ dan $\cap \{A_n : n \in\mathbb{N}\}$

Jawab.
1. Perhatikan bahwa $$A_1 = \{(1+1)k : k\in\mathbb{N} \} = \{2k : k \in \mathbb{N}\} $$dan $$A_2 = \{(2+1)k : k\in\mathbb{N} \} = \{3k : k \in \mathbb{N}\}. $$Dengan kata lain, $A_1$ adalah himpunan bilangan asli kelipatan $2$ dan $A_2$ adalah himpunan semua bilangan asli kelipatan $3.$ Secara umum, $A_{n+1}$ adalah himpunan bilangan asli kelipatan $n.$

Oleh karena itu, $A_1 \cap A_2$ adalah himpunan semua bilangan asli kelipatan $2$ dan $3,$ atau dengan kata lain, himpunan tersebut adalah himpunan semua bilangan asli kelipatan $2\times 3 = 6,$ yaitu $$A_1 \cap A_2 = A_5 = \{5, 10, 15, …\}$$

2. Berdasarkan pemaparan sebelumnya, diperoleh bahwa $A_{n+1}$ adalah himpunan bilangan asli kelipatan $n.$ Oleh karena itu, $$n \in A_{n+1}, \quad n \in \mathbb{N}. $$
Dengan fakta tersebut, akan ditunjukkan bahwa $$\cup \{A_n : n\in \mathbb{N}\} = \mathbb{N} \setminus \{1\} $$dengan menunjukkan bahwa $$\{A_n : n\in \mathbb{N}\} \subseteq \mathbb{N} \setminus \{1\} $$dan $$\mathbb{N} \setminus \{1\} \subseteq \{A_n : n\in \mathbb{N}\}.$$

Misalkan $m \in \cup \{A_n : n\in \mathbb{N}\}.$ Maka, $m \in A_n$ untuk suatu $n \in \mathbb{N}$, yaitu $m$ adalah bilangan asli kelipatan $(n+1)$. Karena $n \in \mathbb{N},$ maka $n+1>1.$ Dari sini, $m$ adalah bilangan asli yang lebih dari $1$ dan berakibat bahwa $$m \in \mathbb{N}\setminus \{1\} $$dan $$\{A_n : n\in \mathbb{N}\} \subseteq \mathbb{N} \setminus \{1\}.$$
Selanjutnya, misalkan $m \in \mathbb{N} \setminus \{a\}.$ Berdasarkan pembahasan sebelumnya, diperoleh bahwa $m \in A_{m+1}.$ Maka, $m \in \cup \{A_n : n\in \mathbb{N}\}$ dan $$\mathbb{N} \setminus \{1\} \subseteq \{A_n : n\in \mathbb{N}\}.$$
Oleh karena itu, $$\cup \{A_n : n\in \mathbb{N}\} = \mathbb{N} \setminus \{1\}. $$

Selanjutnya akan ditunjukkan $$\cap \{A_n : n \in\mathbb{N}\} = \emptyset. $$Sebelumnya, perhatikan bahwa karena untuk setiap bilangan asli $n$ berlaku $A_{n+1}$ adalah himpunan bilangan asli kelipatan $n$, maka $n \notin A_n$ untuk setiap bilangan asli $n.$

Andaikan bahwa $\cap \{A_n : n \in\mathbb{N}\}$ bukan merupakan himpunan kosong. Maka, ada $m \in A_n$ untuk setiap $n \in \mathbb{N}.$ Dari sini, $m \in A_m$ yang kontradiksi dengan fakta sebelumnya. Oleh karena itu, pengandaian salah dan haruslah $$\cap \{A_n : n \in\mathbb{N}\} = \emptyset.$$

Jadi, $$\cup \{A_n : n\in \mathbb{N}\} = \mathbb{N} \setminus \{1\} $$dan $$\cap \{A_n : n \in\mathbb{N}\} = \emptyset.$$

Demikian postingan kali ini tentang Pembahasan Soal Analisis Real Himpunan dan Fungsi bagian 1.1. Postingan ini terkait dengan Pembahasan Soal Analisis real dari buku bartle. Jika Anda tertarik dengan pembahasan soal lainnya, silahkan ke sini. Jika Anda tertarik dengan topik/materi lainnya, silahkan ke sini. Semoga membantu. Sekian dan terima kasih.